Similar to Python lists and tuples, sets are data structures used to store data collection of items. There are some differences. Sets don't allow duplicate values. This makes sets an excellent choice when you need to work with unique items or perform operations like union, intersection, or difference on collections of elements.

Here are some key characteristics of Python sets:

1. Uniqueness: Sets can only contain unique elements. If you try to add a duplicate element, the set won't include it.

2. Mutable: Sets are mutable, meaning you can add or remove elements after creating a set.

3. Unordered: Sets are unordered, so they don't have a defined order. The elements are stored in a way that optimizes set operations.

4. Iterable: You can iterate through the elements of a set using loops or other iterable constructs.

5. Mathematical Operations: Sets support various mathematical operations like union, intersection, difference, and symmetric difference.

Example 1

Type the below code into your editor.

In this example, we create a set called colors containing unique color names. We add the color "purple" to the set, and even though we attempt to add "red" again (which is already in the set), it doesn't result in a duplicate entry. When we print the set, we can see that it only contains unique colors.

The order of elements in the set when printed as {'green', 'purple', 'blue', 'yellow', 'red'} may seem surprising, but it's important to understand that sets in Python are unordered collections. This means that the elements within a set do not have a specific order, and they can be arranged in any way that optimizes internal operations within the set.

Example 2

I trust you have a recollection of set theories; if not, worry not, for the program is designed to be comprehensible with only a minimal grasp of set theories. Please input the following code into your code editor.

Here, two sets, set1 and set2, are created. set1 contains the elements 1, 2, 3, 4, and 5, while set2 contains the elements 3, 4, 5, 6, and 7. Remember that sets only store unique elements, so any duplicate values are automatically removed.

Union of Sets

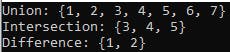
The union() method is used to find the union of two sets. The union of sets contains all the unique elements from both sets. In this code, it combines the elements from set1 and set2 to create a new set called union_result, which contains all unique elements from both sets. The result is printed as "Union," followed by the set itself using an f-string for formatting.

Intersection of Set

The intersection() method finds the intersection of two sets, which contains the elements that are common to both sets. In this code, it finds the common elements between set1 and set2 and stores them in the intersection_result set. The result is printed as "Intersection," followed by the set of common elements.

Difference Between Sets

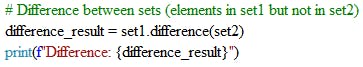
The difference() method computes the difference between two sets. It returns a set that contains the elements from the first set (set1 in this case) that are not present in the second set (set2). The result is stored in the difference_result set and printed as "Difference," followed by the set of differing elements.

When you run this code, you will see the output that shows the results of each set operation (union, intersection, and difference) based on the elements in set1 and set2. These operations are essential for working with sets and are useful for various data manipulation tasks. The f-strings used for formatting make the output more readable by embedding the results directly in the string.

That concludes today's session. I trust that you've gained valuable insights. In our upcoming article, we will delve into the topic of dictionaries. Stay tuned for more.